Research

I have worked on studying the role of turbulence in amplifying magnetic fields in collisionless plasma and have studied the collisionless turbulent dynamo in various regimes using hybrid particle-in-cell simulations. I have also studied the collisional magnetohydrodynamic turbulent dynamo using MHD numerical simulations.

During my PhD, I developed a new hybrid particle-in-cell (hybrid PIC) code called AHKASH, which stands for Astrophysical Hybrid-Kinetic simulations with flASH. AHKASH uses the architecture of the multi-physics FLASH code. This new code uses a Boris particle integrator and a predictor–predictor–corrector algorithm for advancing the hybrid-kinetic equations, using the constraint transport method to ensure that magnetic fields are divergence-free. AHKASH also supports various interpolation schemes between the particles and grid cells, with post-interpolation smoothing to reduce finite particle noise. AHKASH has been tested on standard physical problems such as the motion of charged particles in uniform and spatially varying magnetic fields, the propagation of Alfvén and whistler waves, and Landau damping of ion acoustic waves. We have tested different interpolation kernels (nearest-grid-point, cloud-in-cell, triangular-shaped-cloud) and have also demonstrate the necessity of performing post-interpolation smoothing. We have coupled the TurbGen turbulence driving module to the new hybrid PIC code, allowing us to study plasma turbulence and test the code on the highly complex physical problem of the turbulent dynamo. To investigate steady-state turbulence with a fixed sonic Mach number, it is important to maintain isothermal plasma conditions, which is not possible when turbulence driving is introduced in a collisionless plasma. To mitigate this, we have introduced a novel cooling method for hybrid PIC codes and have provided tests and calibrations of this method to keep the plasma isothermal. This cooling method is demonstrated by the figure below for both subsonic and supersonic plasma. We have also tested the hybrid precision method, which can significantly reduce the computational cost, without compromising the accuracy of the numerical solutions.

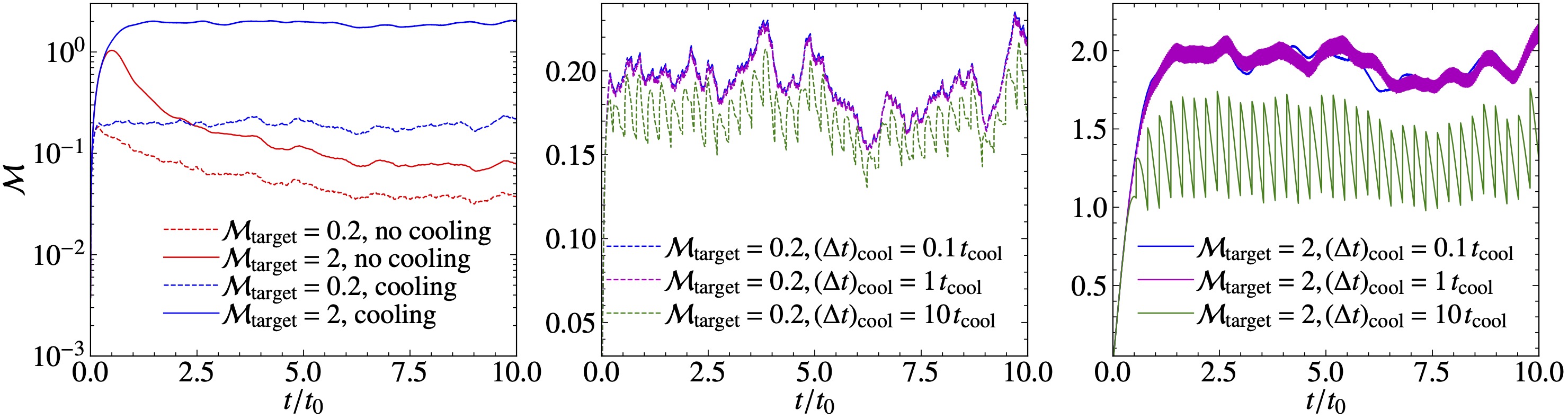
The Mach number (M) as a function of time for subsonic (M = 0.2) and supersonic (M = 2) turbulence driving numerical tests, without and with cooling (left panel), for subsonic (middle panel) and for supersonic tests (right panel) with varying cooling timescales.

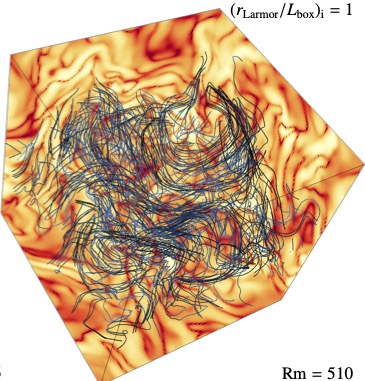Magnetic field streamlines (shown by the blue colored structures inside the box) and magnetic energy (depicted by the yellow-red features) in the exponential growth phase for an initially magnetized collisionless turbulent dynamo simulation with magnetic Reynolds number 500. Small-scale structure in the magnetic energy from the turbulent dynamo action can be seen.

The intracluster medium of galaxy clusters is an extremely hot and diffuse, nearly collisionless plasma, which hosts dynamically important magnetic fields of micro-Gauss strength. Seed magnetic fields of much weaker strength of astrophysical or primordial origin can be present in the intracluster medium. In collisional plasmas, which can be approximated in the magnetohydrodynamical (MHD) limit, the turbulent dynamo mechanism can amplify weak seed fields to strong dynamical levels efficiently by converting turbulent kinetic energy into magnetic energy. However, the viability of this mechanism in weakly collisional or completely collisionless plasma is much less understood.
I have studied the properties of the collisionless turbulent dynamo using three-dimensional hybrid-kinetic particle-in-cell simulations with the AHKASH code. The magnetic Reynolds number is an important parameter for the turbulent dynamo, and it is well-established that for the MHD turbulent dynamo, a critical magnetic Reynolds number exists, above which magnetic field amplification by the turbulent dynamo is possible. We explored the properties of the collisionless turbulent dynamo in the kinematic (exponential growth) phase for different values of the magnetic Reynolds number, initial magnetic-to-kinetic energy ratio, and initial Larmor ratio (the ratio of the Larmor radius to the size of the turbulent system). We found that in the 'un-magnetized' regime, where the initial Larmor ratio is larger than one, the critical magnetic Reynolds number for the dynamo action is 107 ± 3. In the 'magnetized' regime, where the initial Larmor ratio is less than one, we find a marginally higher critical magnetic Reynolds number of 124 ± 8. We found that the growth rate of the magnetic energy does not depend on the strength of the seed magnetic field when the initial magnetization is fixed. We also studied the distribution and evolution of the pressure anisotropy in the collisionless plasma and compared our results with the collisional MHD turbulent dynamo.

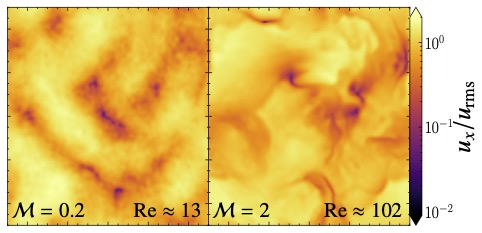The slice plots of velocity for subsonic (left) and supersonic (right) collisionless turbulent dynamo in the kinematic regime. The velocity structures show that the subsonic collisionless plasma is viscous and the supersonic collisionless plasma is more turbulent.

I studied the properties of the collisionless turbulent dynamo in the kinematic growth phase in both the subsonic and the previously unexplored supersonic regime of turbulence, using hybrid PIC simulations. A comparison with the MHD turbulent dynamo reveals significant differences between subsonic and supersonic dynamos, and depends on whether the plasma is described in the MHD approximation or with a kinetic approach. A large parameter study is carried out in which we fix the magnetic Reynolds number, Rm = 500, and vary the kinetic Reynolds number, Re = 500, 50 and 5 for the MHD simulations, while in the hybrid PIC simulations, only Rm=500 is controlled, but Re results self-consistently from wave-particle interactions in the plasma. We find that the magnetic field structure and power spectra of the collisionless turbulent dynamo are similar to that of the MHD turbulent dynamo with Re = 50-500 in both the subsonic and supersonic regimes. In the subsonic case, the velocity structures and turbulent velocity spectra of the collisionless turbulent dynamo are similar to the Re=5-50 MHD turbulent dynamo. In the supersonic case, it is similar to the Re=50-500 MHD turbulent dynamo. Comparing the morphology and power spectra, as well as MHD scaling relations, we infer Re=13 and 102 in the subsonic and supersonic collisionless plasma, respectively, indicating that the properties of turbulence are fundamentally different in collisionless plasma.

Gamma-ray observations of TeV blazars place a lower limit of 10^-18 - 10^-16 Gauss on the intergalactic magnetic field (IGMF) strength in the voids of the Universe on megaparsec scales. Magnetic fields of much weaker strength can be generated at the electroweak and QCD phase transition in the early Universe, and a turbulent small-scale dynamo acting in the primordial Universe can amplify these weak seed magnetic fields. This primordial turbulent dynamo operates in highly subsonic conditions with a sonic Mach number of ~ 10^-4. I performed MHD driven turbulence simulations using the FLASH code in the previously unexplored highly subsonic regime and showed that the purely compressively driven dynamo can be efficient in extremely subsonic plasma.
Turbulence in the early Universe can be driven through compressive velocity fluctuations from primordial density perturbations (PDP) and first-order phase transitions in the early Universe. I applied my results to the baryon-photon fluid before recombination in the early Universe. In case PDP drives turbulence, I showed that the turbulent dynamo can amplify magnetic fields up to 10^-16 Gauss on length scales of 0.1 parsec at the present day. If driven by first-order phase transitions, magnetic fields can be amplified up to 10^-13 Gauss on length scales of 100 parsec at the present day. These values are compatible with the IGMF lower limits inferred from gamma-ray observations on both these scales. This suggests that the origin of IGMF can be from magnetic field amplification by a turbulent dynamo in the early Universe. You can read more about this work here.